Unknown Story
Storyboard Tekst
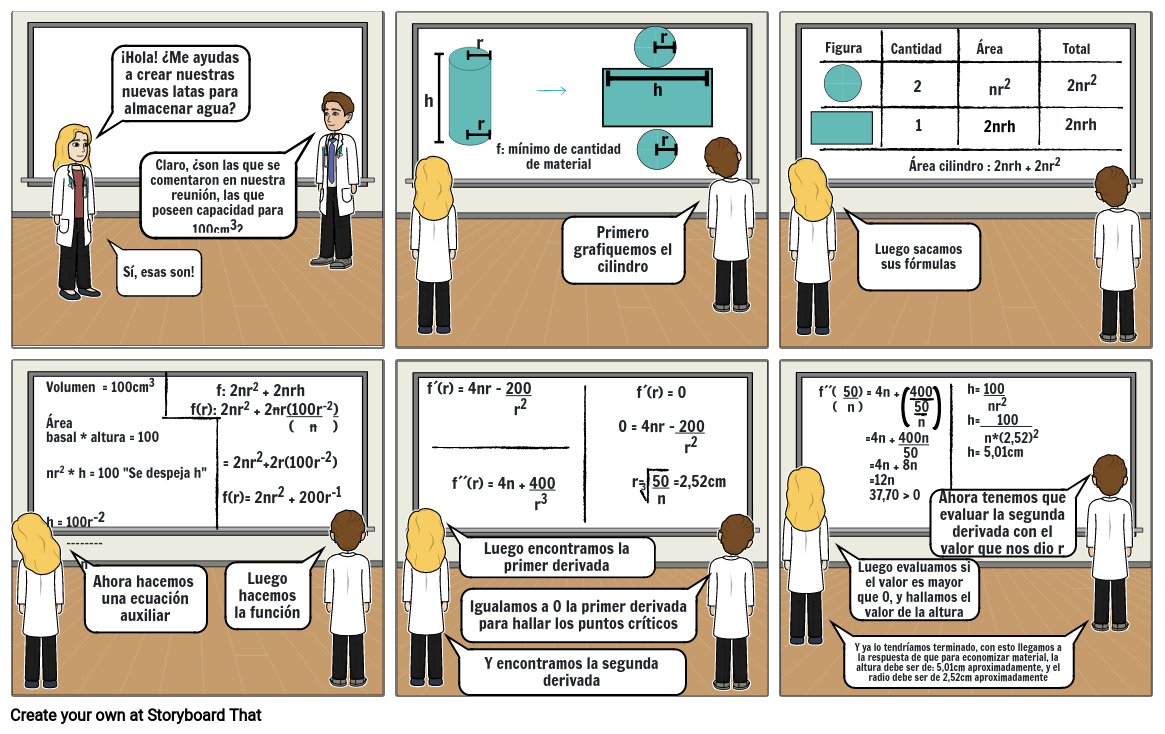
- ¡Hola! ¿Me ayudas a crear nuestras nuevas latas para almacenar agua?
- Sí, esas son!
- Claro, ¿son las que se comentaron en nuestra reunión, las que poseen capacidad para 100cm3?
- h
- r
- r
- f: mínimo de cantidad de material
- Primero grafiquemos el cilindro
- Una vez graficado el cilindro podemos sacar su area sabiendo
- h
- r
- r
- Figura
- Luego sacamos sus fórmulas
- Cantidad
- 2
- 1
- Área cilindro : 2nrh + 2nr2
- Área
- nr2
- 2nrh
- Total
- 2nrh
- 2nr2
- Volumen = 100cm3Área basal * altura = 100nr2 * h = 100 "Se despeja h"h = 100r-2 -------- n
- Ahora hacemos una ecuación auxiliar
- f: 2nr2 + 2nrh f(r): 2nr2 + 2nr(100r-2) ( n ) = 2nr2+2r(100r-2) f(r)= 2nr2 + 200r-1
- Luego hacemos la función
- f´(r) = 4nr - 200 r2
- f´´(r) = 4n + 400 r3
- Y encontramos la segunda derivada
- Luego encontramos la primer derivada
- Igualamos a 0 la primer derivada para hallar los puntos críticos
- f´(r) = 00 = 4nr - 200 r2 r= 50 =2,52cmn
- 3
- f´´( 50) = 4n + 400 ( n ) 50 n
- Y ya lo tendríamos terminado, con esto llegamos a la respuesta de que para economizar material, la altura debe ser de: 5,01cm aproximadamente, y el radio debe ser de 2,52cm aproximadamente
- Luego evaluamos si el valor es mayor que 0, y hallamos el valor de la altura
- =4n + 400n 50
- =4n + 8n=12n37,70 > 0
- Ahora tenemos que evaluar la segunda derivada con el valor que nos dio r
- h= 100 nr2h= 100 n*(2,52)2h= 5,01cm
Meer dan 30 miljoen storyboards gemaakt

