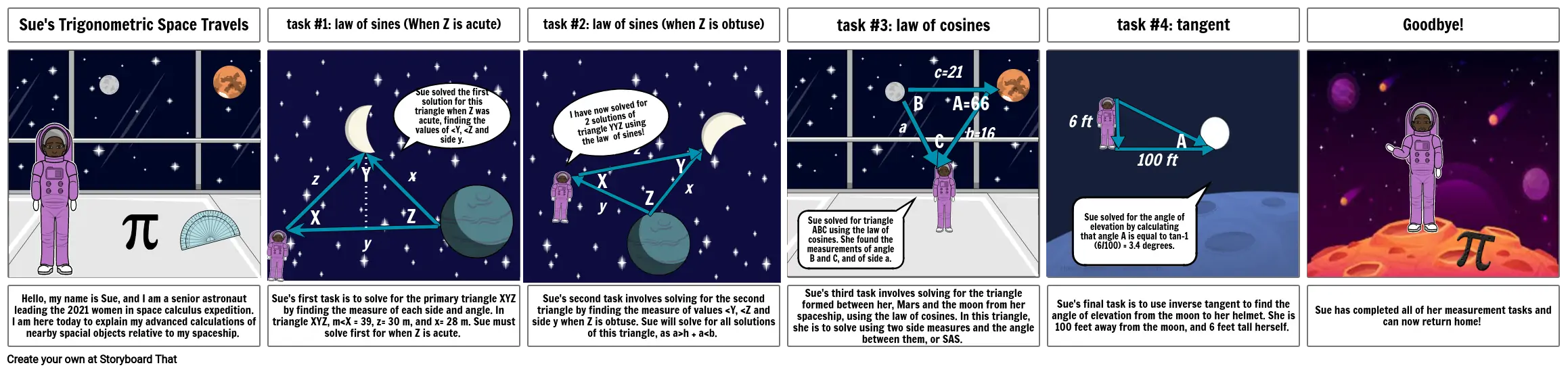
Sue's Trigonometric Space Travel
Opis Storyboarda
Read as Sue travels through space, calculating the proximity of her stellar findings along the way.
Storyboard Tekst
- Sue's Trigonometric Space Travels
- task #1: law of sines (When Z is acute)
- z
- X
- Y
- y
- x
- Z
- Sue solved the first solution for this triangle when Z was acute, finding the values of <Y, <Z and side y.
- task #2: law of sines (when Z is obtuse)
- I have now solved for 2 solutions of triangle YYZ using the law of sines!
- y
- X
- z
- Z
- Y
- x
- task #3: law of cosines
- Sue solved for triangle ABC using the law of cosines. She found the measurements of angle B and C, and of side a.
- a
- B
- C
- c=21
- A=66
- b=16
- task #4: tangent
- 6 ft
- Sue solved for the angle of elevation by calculating that angle A is equal to tan-1 (6/100) = 3.4 degrees.
- 100 ft
- A
- Goodbye!
- Hello, my name is Sue, and I am a senior astronaut leading the 2021 women in space calculus expedition. I am here today to explain my advanced calculations of nearby spacial objects relative to my spaceship.
- Sue's first task is to solve for the primary triangle XYZ by finding the measure of each side and angle. In triangle XYZ, m<X = 39, z= 30 m, and x= 28 m. Sue must solve first for when Z is acute.
- Sue's second task involves solving for the second triangle by finding the measure of values <Y, <Z and side y when Z is obtuse. Sue will solve for all solutions of this triangle, as a>h + a<b.
- Sue's third task involves solving for the triangle formed between her, Mars and the moon from her spaceship, using the law of cosines. In this triangle, she is to solve using two side measures and the angle between them, or SAS.
- Sue's final task is to use inverse tangent to find the angle of elevation from the moon to her helmet. She is 100 feet away from the moon, and 6 feet tall herself.
- Sue has completed all of her measurement tasks and can now return home!
Izrađeno više od 30 milijuna scenarija

