El uso de las analogías
Storyboard Text
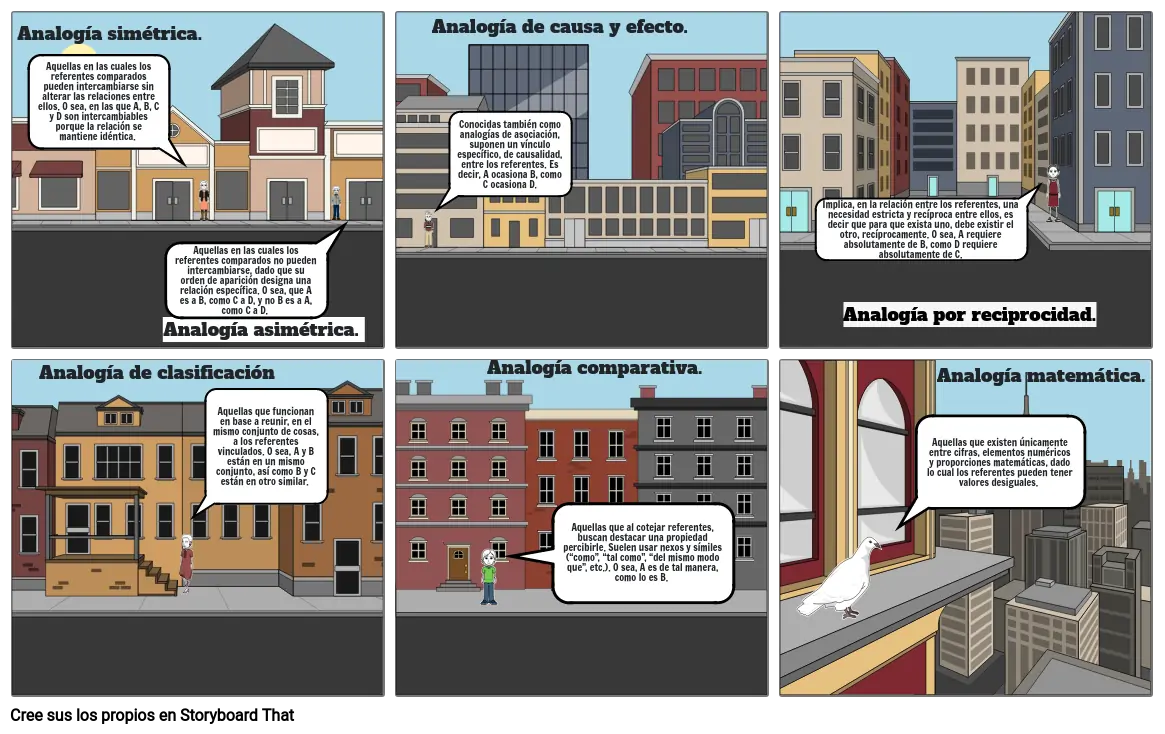
- Analogía simétrica.
- Analogía de clasificación
- Aquellas en las cuales los referentes comparados pueden intercambiarse sin alterar las relaciones entre ellos. O sea, en las que A, B, C y D son intercambiables porque la relación se mantiene idéntica.
- Analogía asimétrica.
- Aquellas en las cuales los referentes comparados no pueden intercambiarse, dado que su orden de aparición designa una relación específica. O sea, que A es a B, como C a D, y no B es a A, como C a D.
- Analogía de causa y efecto.
- Conocidas también como analogías de asociación, suponen un vínculo específico, de causalidad, entre los referentes. Es decir, A ocasiona B, como C ocasiona D.
- Analogía comparativa.
- Analogía por reciprocidad.
- Implica, en la relación entre los referentes, una necesidad estricta y recíproca entre ellos, es decir que para que exista uno, debe existir el otro, recíprocamente. O sea, A requiere absolutamente de B, como D requiere absolutamente de C.
- Analogía matemática.
- Aquellas que funcionan en base a reunir, en el mismo conjunto de cosas, a los referentes vinculados. O sea, A y B están en un mismo conjunto, así como B y C están en otro similar.
- Aquellas que al cotejar referentes, buscan destacar una propiedad percibirle. Suelen usar nexos y símiles (“como”, “tal como”, “del mismo modo que”, etc.). O sea, A es de tal manera, como lo es B.
- Aquellas que existen únicamente entre cifras, elementos numéricos y proporciones matemáticas, dado lo cual los referentes pueden tener valores desiguales.
Vytvořeno více než 30 milionů Storyboardů

